Additive Rotary Embedding - A Competitive Alternative to RoPE

Introduction

Rotary Embedding (RoPE) is a relative positional embedding widely used by most language models. [1]

The idea behind RoPE is to find a function \(f\) such that the dot-product between \(f(\mathbf{q}, m)\) and \(f(\mathbf{k}, n)\) is a function of \(m - n\). [2]

\[\begin{equation} \langle f(\mathbf{q}, m), f(\mathbf{k}, n) \rangle = g(\mathbf{q}, \mathbf{k}, m - n) \tag{1} \end{equation}\]

And RoPE is a function that satisfies the above condition and works well in practice.

---

I find rotary embedding easier to understand if we view q (query) and k (key) as tensor of complex numbers. [3]

When viewed at one channel at a time, it’s simply:

q_i_rope = q_i * torch.polar(1, theta * i)
k_j_rope = k_j * torch.polar(1, theta * j)

where theta is the frequency of the channel, and i, j are the position of q and k, respectively. Each channel has a different pre-defined frequency.

---

Although RoPE elegantly satisfies the condition in equation (1), it’s not very intuitive and it has some drawbacks.

1. When the relative rotation is 180 degrees, the dot-product is flipped, which feels unnatural?
2. In addition to the above, there is also no way to attend without the interaction of the relative position j-i.
3. Actually, model can learn to “ignore” certain frequency by minimizing the magnitude of the projection matrix related to that frequency. But that seems inefficient.
4. (hypothesis) The model might need to encode the same information in different frequencies (redundant) to avoid the above problems.

In fact, EleutherAI’s experiment shows that partial RoPE can achieve better performance. And some models also uses it intentionally, like Pythia, Phi-2.

references:

• [1] Rotary Embedding paper (RoFormer: Enhanced Transformer with Rotary Position Embedding): https://arxiv.org/abs/2104.09864

• [2] Eleuther’s blog post on rotary embeddings: https://blog.eleuther.ai/rotary-embeddings/

• [3] Mistral’s reference implementation, which uses complex numbers for some RoPE operations: https://github.com/mistralai/mistral-inference/blob/main/one_file_ref.py

Additive Rotary Embedding

Motivated by the above observations, we can modify RoPE to allow turning off the interaction of relative position, by making it additive, and adding learnable weights:

q_i_rope = q_i + weight_q * torch.polar(1, theta * i)
k_j_rope = k_j + weight_k * torch.polar(1, theta * j)

Additionally, we can add a learnable offset to each frequency, to learn different phases, which RoPE can learn implicitly in the projection matrix.

q_i_rope = q_i + weight_q * torch.polar(1, theta * i + offset_q)
k_j_rope = k_j + weight_k * torch.polar(1, theta * j + offset_k)

I call this Additive Rotary Embedding (AddRoPE).

---

Finally, if we look at Sinusoidal positional encoding from Attention is all you need and view it as complex numbers, it can be seen as:

x = x + torch.polar(1, theta * i)

where x is 2-dimensions of input embedding, viewed as one complex number, and theta is the frequency of one channel.

So Additive Rotary Embedding can be seen as a generalization of Sinusoidal positional encoding. Where the encoding is applied to q and k at each layer, with additional learnable parameters.

Implementation & Performance

Because we have a learnable offset, we can’t cache the rotation vectors during training. But we also won’t need to rotate the q/k vectors (multiplications).

For 1 attention head, Q/K is of shape [batch_size, seq_len, head_dim] = [B, L, H]

• In RoPE, we need to do 2BLH multiplications for q and k each, totaling 4BLH multiplications.
• In AddRoPE, we don’t have multiplication outside of the learnable offset, which is of shape [L, H]

In practice it is slighlty faster then RoPE, even if B is small. Furthermore, during inference, the additive rotation vectors can be pre-computed.

Experiments

• I trained GPT-2 (124M & 355M) model on fineweb 10B subset, using RoPE and AddRoPE, and the results are comparable.
• On the 124M model, AddRoPE is slightly worse than RoPE, but on the 355M model, AddRoPE eventually outperforms RoPE slightly.

image.png

Visualization

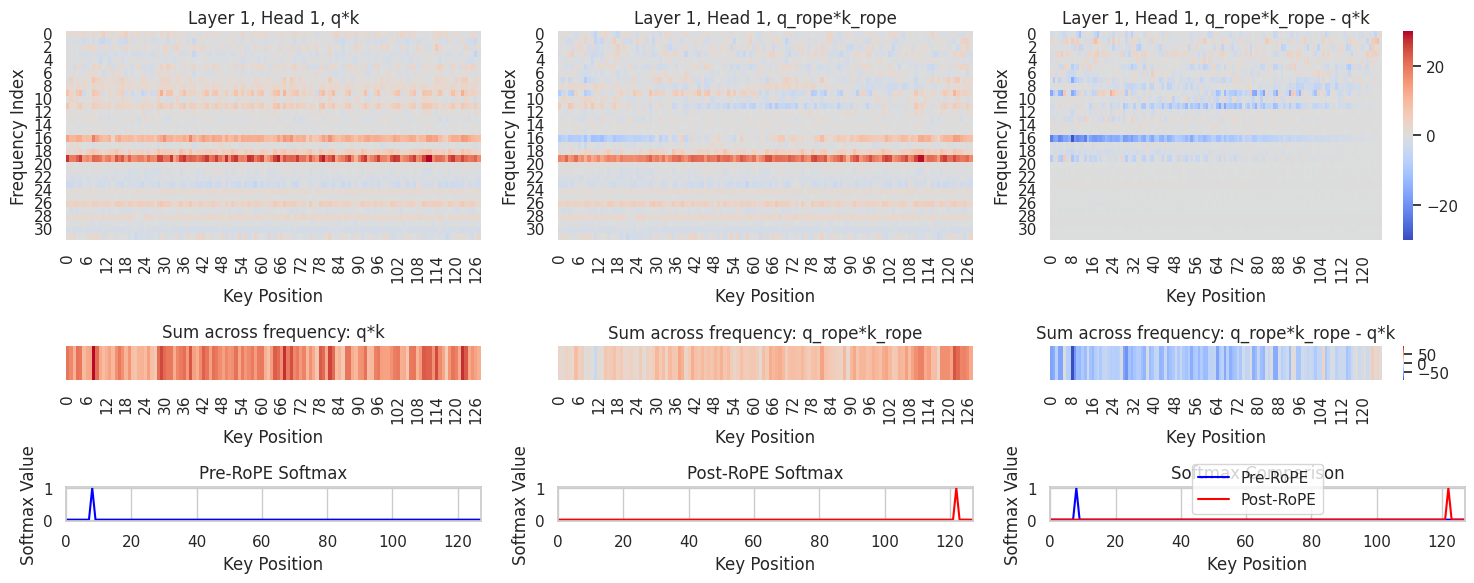
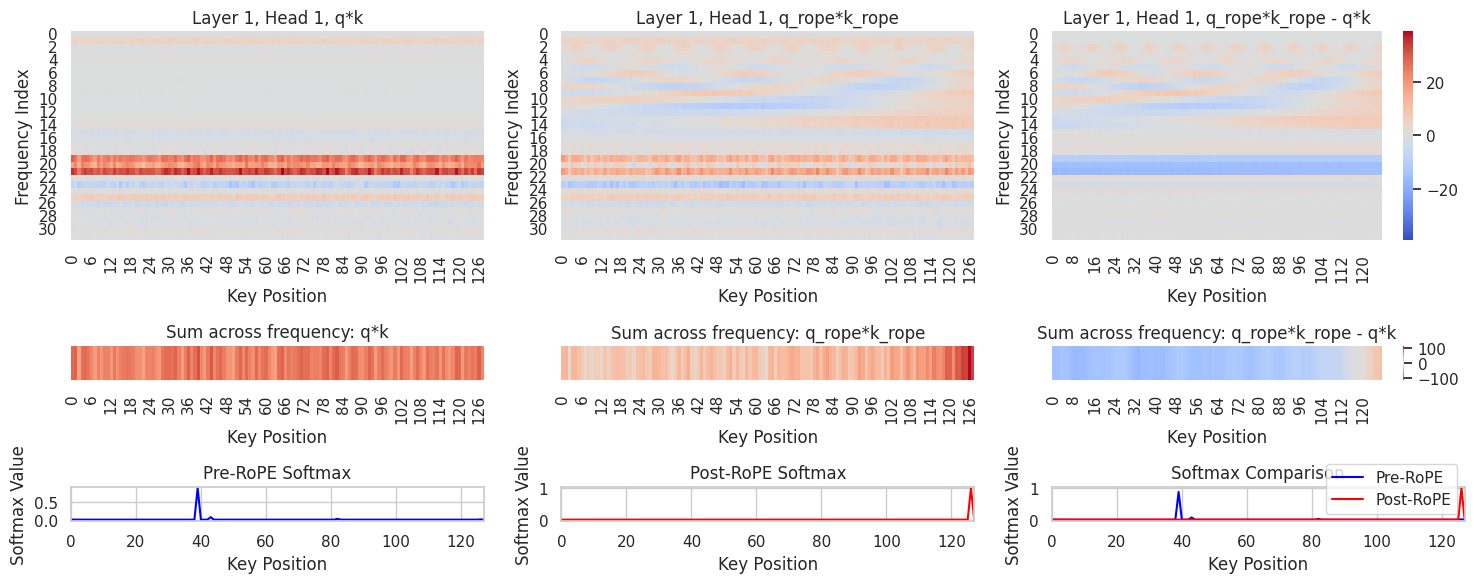
Here the visualization shows the difference RoPE and AddRoPE make: \(\langle f(q), f(k) \rangle - \langle q, k \rangle\)

• Here the Query position is fixed. x-axis is the Key position, and y-axis is the channel index (different frequencies).

• RoPE:

  • The difference has some wave-like patterns, but it’s noisy.

• AddRoPE:

  • The difference is much smoother. Also the first few frequencies have very small contribution in this attention head. Suggesting the model can learn to ignore certain frequencies.

Conclusion

• Additive Rotary Embedding is a competitive alternative to Rotary Embedding.
• It is also a generalization of Sinusoidal positional encoding.
• It’s an absolute positional encoding, but with a very strong relative inductive bias.
• Unlike RoPE, it can learn to discard certain frequencies, without zeroing out that channel.
• It’s slightly faster than RoPE in practice.

Absolute vs Relative

In my limited testing, it can outperform RoPE in terms of extrapolating to unseen sequence length (without fine-tuning or scaling).

In practice, with scaling and continue pre-training to adapt to longer sequence length, I expect it to be able to generalize to longer sequence length like RoPE.